This project is about estimating (predicting) the interaction vertex with Deep Neural Network (DNN). We intend to use this method to reconstruct the interaction vertex in SpinQuest experiment at Fermilab. The code framework for the analysis is located in one of my GitHub repository.

Motivation

A solid iron beam dump, approximately 5 meters in length (referred to as FMAG), is situated between the spectrometers and the target of SpinQuest experiment of Fermilab. Its purpose is to capture all undesired particles generated in the target area, excluding muon particles. However, the presence of this lengthy solid iron structure poses challenges in accurately reconstructing the interaction vertex. Currently, a vertexing algorithm based on the Kalman filter is employed to reconstruct the vertex using track information obtained from detectors downstream of FMAG. In this study, we explored the use of a Machine Learning approach to identify the interaction vertex instead.

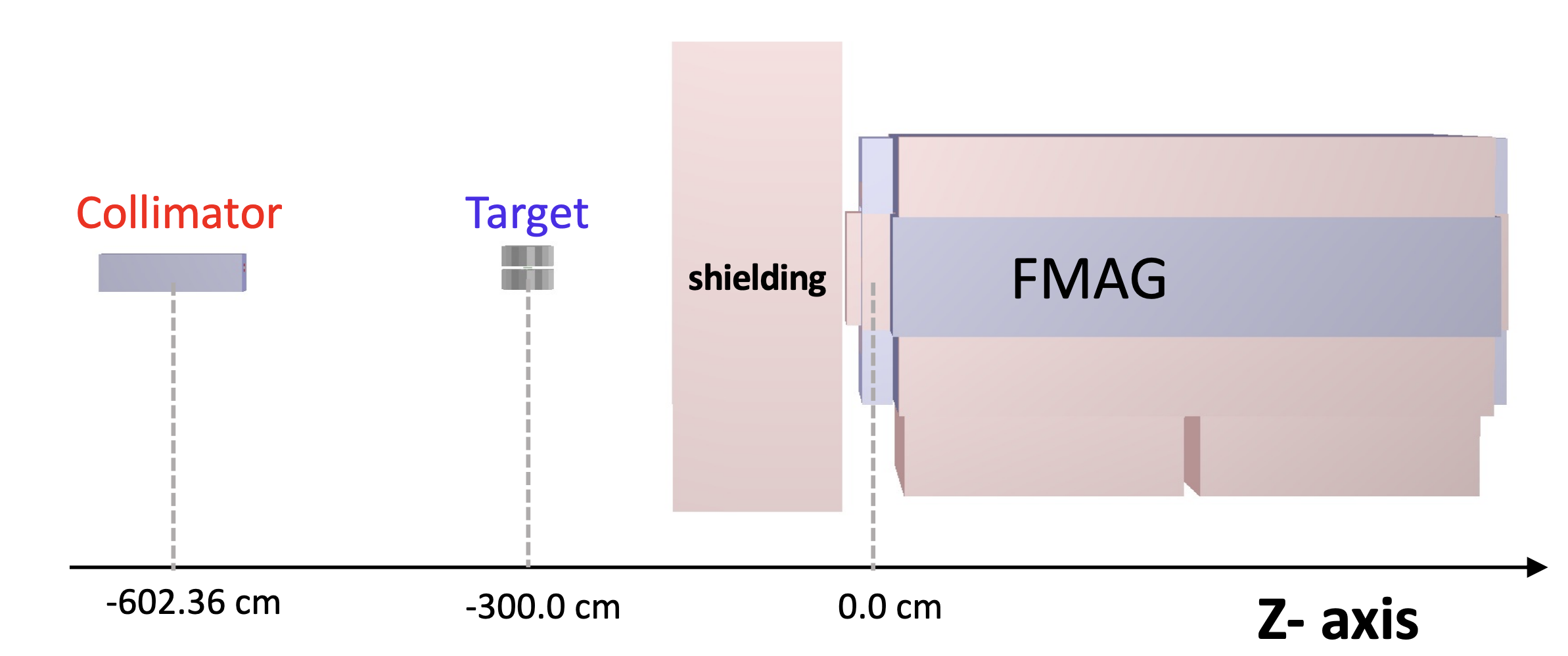
Fig.1 - Beam line volumes in SpinQuest Experiment.

Data

Monte Carlo simulated Raw data for SpinQuest was used for the analysis. Raw data contains ~200k Drell-Yan events with $\mu^{+/-}$ particles’ information. The structure of the input data is;

X = [charge, station1[x, y, z], station1[x, y, z], station3[px, py, pz], station3[px, py, pz]]
y = [vertex[x, y, z, px, py, pz]]

Machine Learning Model

* * * * * *     * * * * * * * * * * * * * * *     * * * * * * * * * * * * * * *     * * * * * *
* Input   *     * Classification Layer      *     * Regression layer          *     *         *
* Tensor  * --> * 2 Linear hidden layers    * --> * 3 Linear hidden layers    * --> * Target  *
*         *     * ReLu activation function  *     * ReLu activation function  *     * Tensor  *
* * * * * *     * CrossEntropyLoss          *     * MSELoss                   *     * * * * * *
                * Adam optimizer            *     * Adam optimizer            *
                * * * * * * * * * * * * * * *     * * * * * * * * * * * * * * *

The Neural Network architecture includes a classification layer and a regression layer. The classification layer is designed to predict the region of interaction, which includes the collimator, air between the collimator and target, target, air between the target and FMAG, and FMAG.

• 0: Collimater
• 1: Air between collimator and target
• 2: Target
• 3: Air between target and FMAG
• 4: FMAG

The shielding is not considered as it contains a hole large enough not to generate any interaction which can be detected in spectrometers.

After the classification layer, a regression layer is implemented to predict the position (X, Y, Z) of the interaction. The overall architecture of the neural network is depicted as shown above.

Analysis

The dataset is splitted into train:validation:test sets with ratio 60:40:40. The accuracy and loss from the classification layers as a funtion of epoch is as shown in Fig. 2, while for the regression layer is shown in Fig. 2.

Fig. 2: Loss and Accuracy for the Classificatin part

Fig. 3: Loss for the Regression part

Results and Conclusion

The ROC-curves and confusion matrix for the classification layer with test set is as shown in Fig. 4 and Fig. 5 respectively.

Fig. 4: ROC curve for test set in Classificatin part

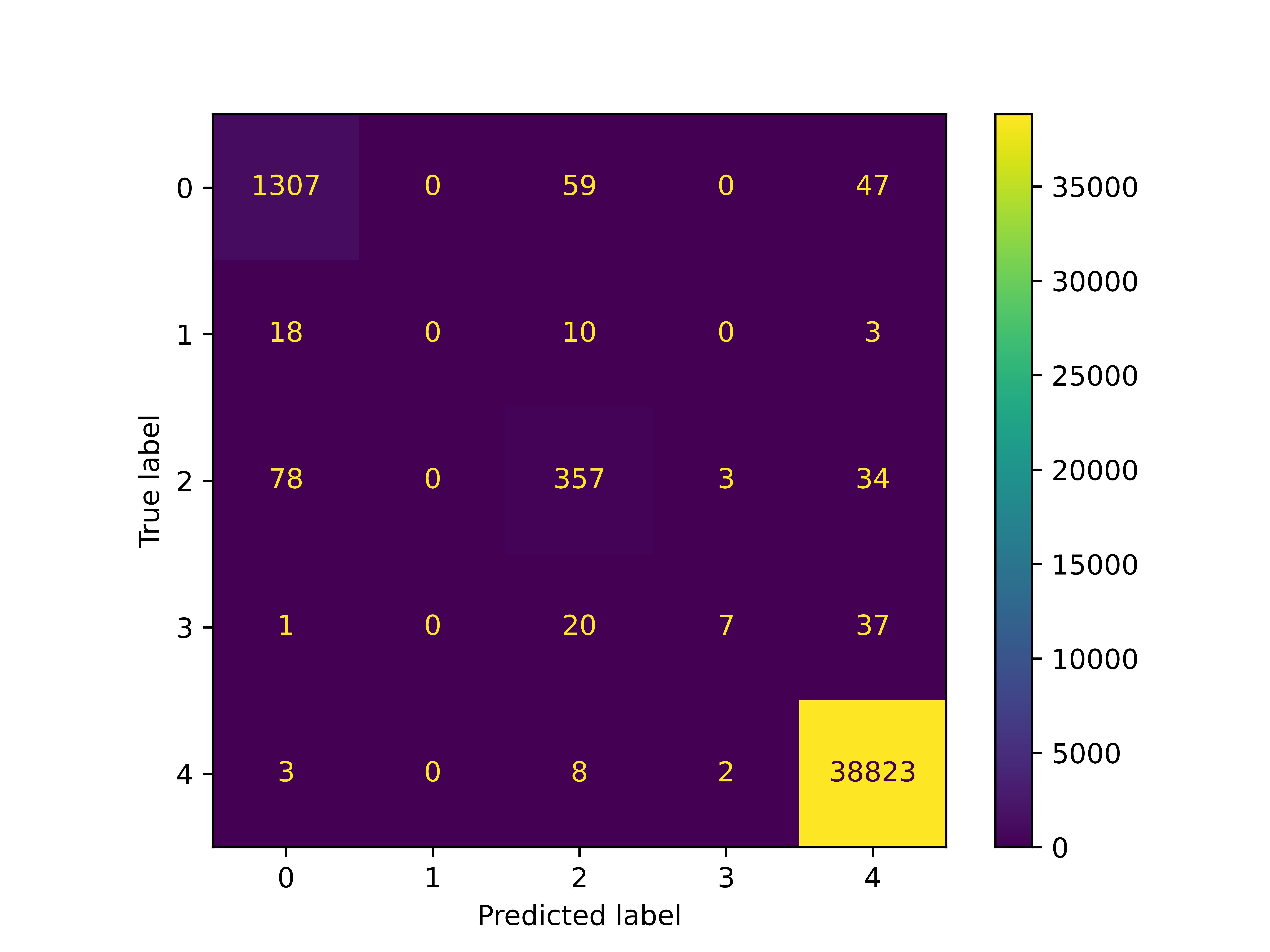
Fig. 5: Confusion Matrix for test set in Classificatin part

The resolution of the (X,Y,Z) interaction vertices from the ML method compared to conventional kalman-filter based vertexing algorithm are as shown in figures below.

Fig. 6: Comparison of difference between truth and predicted X-, Y- and Z- from ML method and those from conventional Kalman Filter method.

From the result, we can see that the ML method clearly outperforms to find the position (both mean and width of difference).

Outlook

The study can be extended to analyze more realistic data with embedding of hits.