Estimating Background with GPR
This project is about estimating the background in the data with Gaussian Process Regression (GPR) method. We intend to use this method in the $J/\psi$ analysis from SeaQuest and SpinQuest experiment at Fermilab. The code framework for the analysis is located in one of my GitHub repository.
Gaussian Process Regression
Gaussian Process Regression (GPR) is a powerful statistical modeling technique used for regression analysis. It is a non-parametric Bayesian approach that can effectively capture complex patterns and relationships in data.
In GPR, the underlying assumption is that the data points are drawn from a Gaussian process, which is a collection of random variables where any finite subset follows a multivariate Gaussian distribution. This makes GPR a flexible and versatile method for modeling various types of data. The key idea behind GPR is to model the relationship between input variables (predictors) and output variables (response) as a continuous function. Unlike traditional regression methods that assume a fixed functional form, GPR provides a flexible framework that can adapt to the data by capturing both the mean and uncertainty in the predictions.
Peak Signal and Background
The $J/\psi$ particle, also known as the $J/\psi$ meson, is a subatomic particle that belongs to the category of mesons with mass 3.14 GeV. Studying the properties and behavior of the $J/\psi$ particle provides valuable insights into the strong nuclear force and the interactions between quarks. It has contributed to our understanding of particle physics, the quark model, and the fundamental building blocks of matter.
The $J/\psi$ particle is unstable and quickly decays into lighter particles. Its decay modes also include the production of muons and antimuons, a dimuon. We can investigate about the $J/\psi$ particle by studying the 3.14 GeV dimouns produced at any nuclear experiment. But in such experiments, along with the $J/\psi$ dimuons, many other dimuons from different physics (or non-physics) process can also be prodcued. Thus the underneath the $J/\psi$ peak of the dimuon mass spectrum, there are some background those need to be subtracted. The background might not have any particular shape and might depend on various kinematics. So,we use GPR method to extract such background underneath the peak.
Data
Toy (unlabeled) data and MonteCarlo Simulated data from SeaQuest Experiment at Fermilab is used for the analysis.
Analysis Steps
The dimuon spectrum of total data (toy) is shown in blue histogram of Fig.1. We are interested to extract signal information from peak region.
Fig.1 - Steps of predicting background underneath a peak signal with GPR.
Take two Side Bands from either sides of $J/\psi$ peak
The two side bands, [1.8, 2.5] GeV and [4.5, 7.] GeV, are taken to train the GPR. The side bands are shown in red shadow region in Fig.1. We should make sure that these side bands don’t contain any signal we are interested i.e. from $J/\psi$. One should keep in mind of the detector resolution and reconstruction performance before choosing such side bands.
Fit GPR with Side Band Data
Now the side bands’ data are used to train the GPR model. The Scikit-Learn package is used to implement the GPR method. The kernal used is product of Constant and RBF (Radial Basis Function).
$K(x_i, x_j) = exp(\frac{d(x_i,x_j)^2}{2l^2})$
where $l$ is length scale and $d(.,.)$ is ecludian distance.
from sklearn.gaussian_process.kernels import RBF, ConstantKernel as C sideband_kernel = C(50000.0, (1e-10, 1e15))*RBF(length_scale=5, length_scale_bounds=(1e-4, 1e15)) gaussian_process = GaussianProcessRegressor(kernel=sideband_kernel, alpha=Y_train_error**2, n_restarts_optimizer=5000) gaussian_process.fit(np.atleast_2d(X_train).T, Y_train)Predict the background underneath the peak with GPR
Y_pred, cov_matrix = gaussian_process.predict(np.atleast_2d(data[:, 0]).T, return_cov=True)The mean prediction from GPR is as shown in dotted oragne line while the orange shadow shows the 95% confidence interval. Thus predicted background is subtracted from total data to get the desired peak signal data as shown in purple line in the Fig.1.
Sanity Check with MonteCarlo
The background underneath the signal is mostly from the another physics process called Drell-Yan. For the sanity check of our method, Drell-Yann dimuon mass spectrum from MonteCarlo simulation were analyzed at different kinematics. GPR method with same side bands was used for the analysis. The GPR was able to predict (oragne dotted) the shape and magnitude of the Drell-Yan mass spectrum in the peak region as shown in Fig.2 and Fig.3.
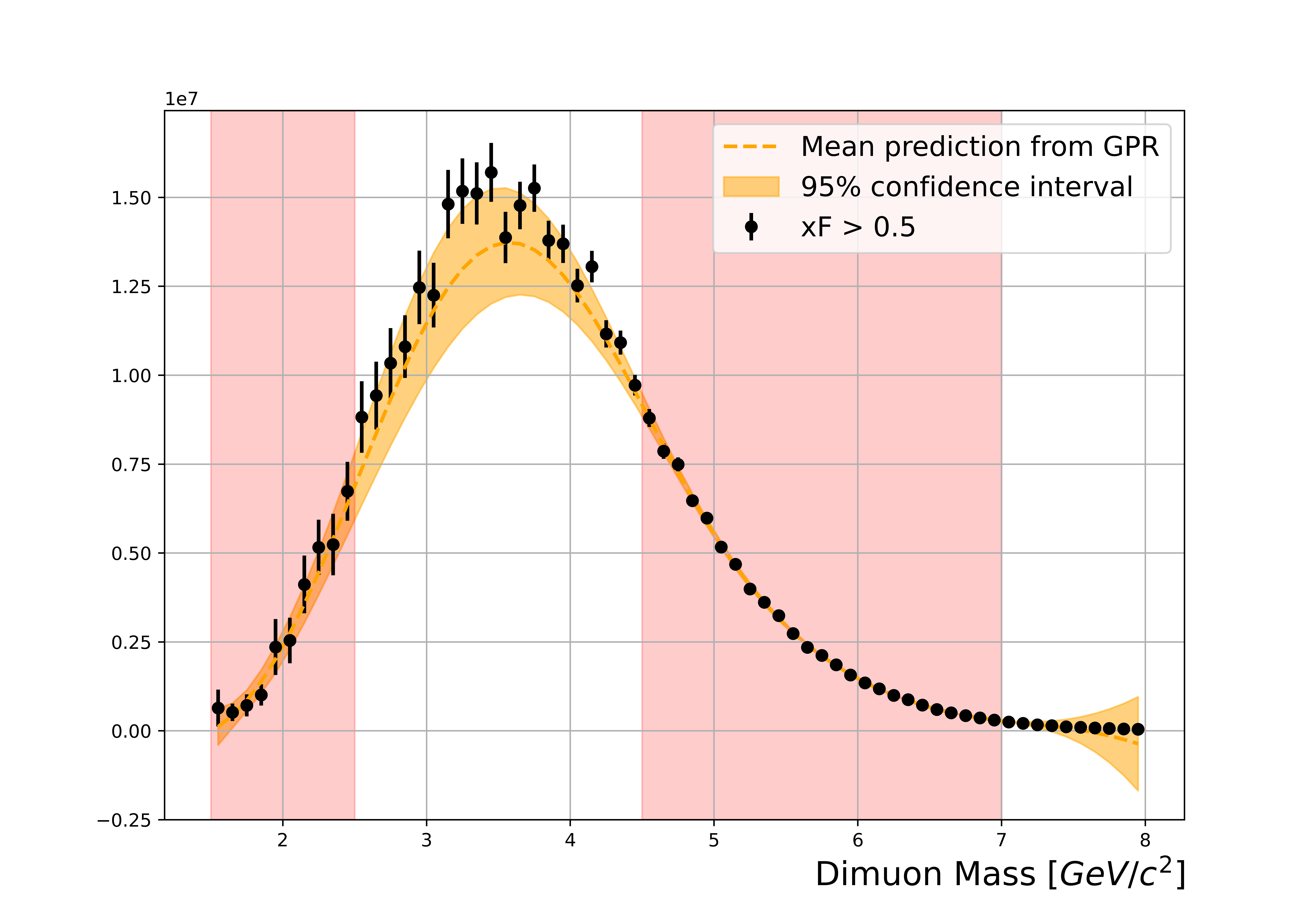
Fig.2 - Drell-Yan mass spectrum (at low xF) at peak signal region is properly predicted by GPR
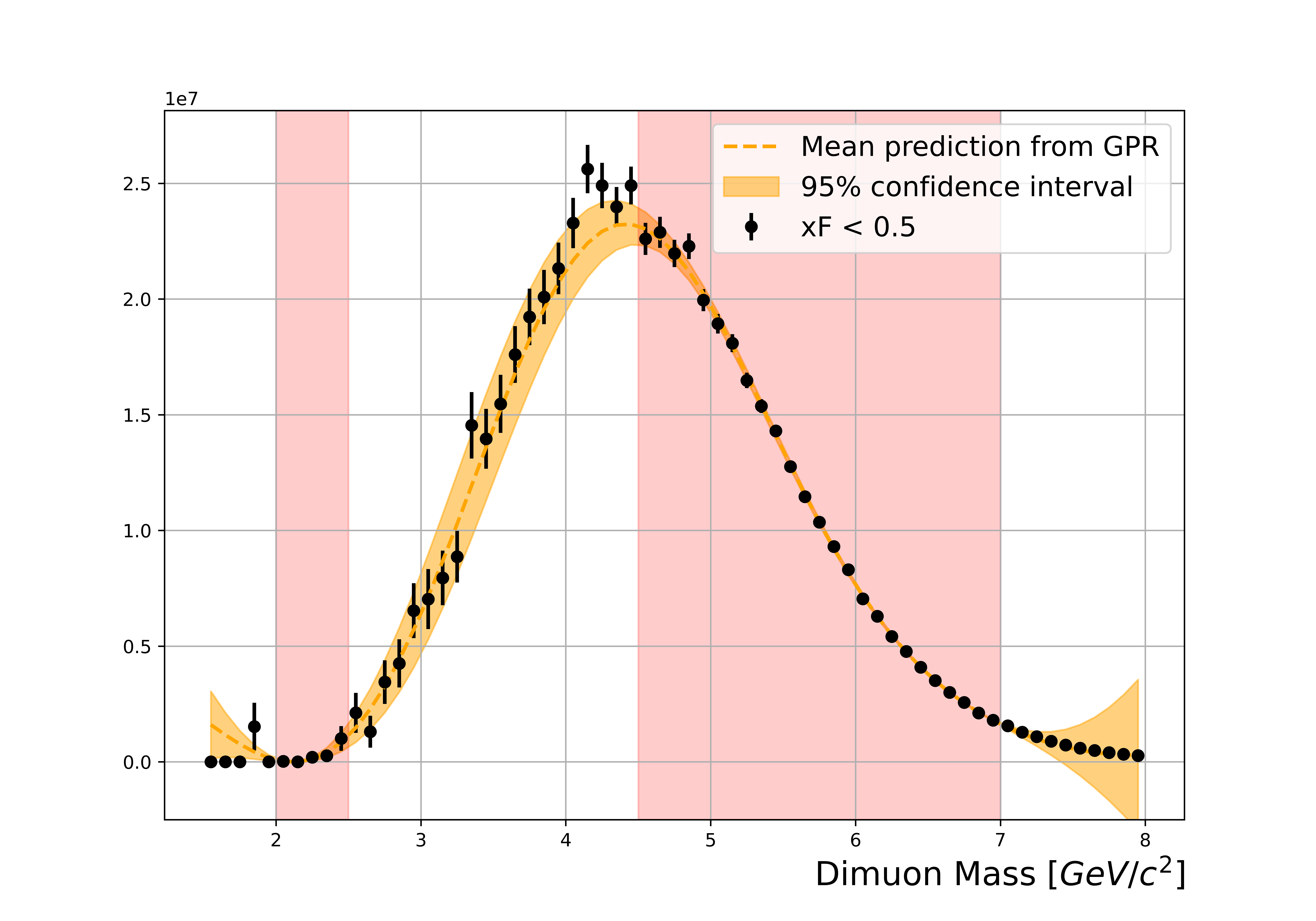
Fig.3 - Drell-Yan mass spectrum (at low xF) at peak signal region is properly predicted by GPR
Outlook
The GreadSearchCV to get the tune the hyparameters to finalize the GPR model. This method will be used for the analysis of $J/\psi$ from SeaQuest and SpinQuest experiment at Fermilab.