Recursive Algorithms

Definition

• An algorithm that calls itself in its definition.
  • Recursive case a conditional statement that is used to trigger the recursion.
  • Base case a conditional statement that is used to break the recursion.

What you need to know

• Stack level too deep and stack overflow.
  • If you’ve seen either of these from a recursive algorithm, you messed up.
  • It means that your base case was never triggered because it was faulty or the problem was so massive you ran out of alloted memory.
  • Knowing whether or not you will reach a base case is integral to correctly using recursion.
  • Often used in Depth First Search

Iterative Algorithms

Definition

• An algorithm that is called repeatedly but for a finite number of times, each time being a single iteration.
  • Often used to move incrementally through a data set.

What you need to know

• Generally you will see iteration as loops, for, while, and until statements.
• Think of iteration as moving one at a time through a set.
• Often used to move through an array.

Recursion Vs. Iteration

• The differences between recursion and iteration can be confusing to distinguish since both can be used to implement the other. But know that,
  • Recursion is, usually, more expressive and easier to implement.
  • Iteration uses less memory.
• Functional languages tend to use recursion. (i.e. Haskell)
• Imperative languages tend to use iteration. (i.e. Ruby)
• Check out this Stack Overflow post for more info.

Pseudo Code of Moving Through an Array

Recursion                         | Iteration
----------------------------------|----------------------------------
recursive method (array, n)       | iterative method (array)
  if array[n] is not nil          |   for n from 0 to size of array
    print array[n]                |     print(array[n])
    recursive method(array, n+1)  |
  else                            |
    exit loop                     |

Greedy Algorithms

Definition

• An algorithm that, while executing, selects only the information that meets a certain criteria.
• The general five components, taken from Wikipedia:
  • A candidate set, from which a solution is created.
  • A selection function, which chooses the best candidate to be added to the solution.
  • A feasibility function, that is used to determine if a candidate can be used to contribute to a solution.
  • An objective function, which assigns a value to a solution, or a partial solution.
  • A solution function, which will indicate when we have discovered a complete solution.

What you need to know

• Used to find the expedient, though non-optimal, solution for a given problem.
• Generally used on sets of data where only a small proportion of the information evaluated meets the desired result.
• Often a greedy algorithm can help reduce the Big O of an algorithm.

Pseudo Code of a Greedy Algorithm to Find Largest Difference of any Two Numbers in an Array.

greedy algorithm (array)
  var largest difference = 0
  var new difference = find next difference (array[n], array[n+1])
  largest difference = new difference if new difference is > largest difference
  repeat above two steps until all differences have been found
  return largest difference

This algorithm never needed to compare all the differences to one another, saving it an entire iteration.

Search Algorithms

Breadth First Search (BFS)

Definition

• An algorithm that searches a tree (or graph) by searching levels of the tree first, starting at the root.
  • It finds every node on the same level, most often moving left to right.
  • While doing this it tracks the children nodes of the nodes on the current level.
  • When finished examining a level it moves to the left most node on the next level.
  • The bottom-right most node is evaluated last (the node that is deepest and is farthest right of it’s level).
• Level order traversal: Start from the root, scan all nodes in a level, then move to the next level, and iterate this process.
• Implementation: Queue (children should wait until all of their parent and its sibling(s) is popped out, see the code below)

What you need to know

• Optimal for searching a tree that is wider than it is deep.
• Uses a queue to store information about the tree while it traverses a tree.
  • Because it uses a queue it is more memory intensive than depth first search.
  • The queue uses more memory because it needs to stores pointers

Time Complexity

• Search: Breadth First Search: O(V + E)
• Eis number of edges
• V is number of vertices

The implementation is here.

Depth First Search (DFS)

Definition

• An algorithm that searches a tree (or graph) by searching depth of the tree first, starting at the root.
  • It traverses left down a tree until it cannot go further.
  • Once it reaches the end of a branch it traverses back up trying the right child of nodes on that branch, and if possible left from the right children.
  • When finished examining a branch it moves to the node right of the root then tries to go left on all it’s children until it reaches the bottom.
  • The right most node is evaluated last (the node that is right of all it’s ancestors).
• Variation
  • Pre-order traversal: Self &rarr Left child &rarr Right child
  • In-order traversal: Left child &rarr Self &rarr Right child
  • Post-order traversal: Left child &rarr Right child &rarr Self
• Implementation: Recursive algorithm or Stack (The deeper the node, the closer to the top in a stack. Then once the deepest node is searched, it is popped out).

What you need to know

• Optimal for searching a tree that is deeper than it is wide.
• Uses a stack to push nodes onto.
  • Because a stack is LIFO it does not need to keep track of the nodes pointers and is therefore less memory intensive than breadth first search.
  • Once it cannot go further left it begins evaluating the stack.

Time Complexity

• Search: Depth First Search: O(|E| + |V|)
• E is number of edges
• V is number of vertices

The implementation is here.

Breadth First Search Vs. Depth First Search

• The simple answer to this question is that it depends on the size and shape of the tree.
  • For wide, shallow trees use Breadth First Search
  • For deep, narrow trees use Depth First Search

Nuances

• Because BFS uses queues to store information about the nodes and its children, it could use more memory than is available on your computer. (But you probably won’t have to worry about this.)
• If using a DFS on a tree that is very deep you might go unnecessarily deep in the search. See xkcd for more information.
• Breadth First Search tends to be a looping algorithm.
• Depth First Search tends to be a recursive algorithm.

Sorting Algorithms

Sort makes searches faster. Let’s cover famous sorting algorithms with their complexity and implementation. Implementation can vary a little, but the complexity in big O won’t vary.

Evaluation of sort algorithms

• Number of comparison
• Number of moves

Bubble sort

Compare two adjacent elements then sort these two. Iterate this process side by side until the end of the array, then iterate again from the beginning until all elements are sorted.

Visualization

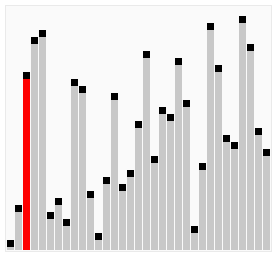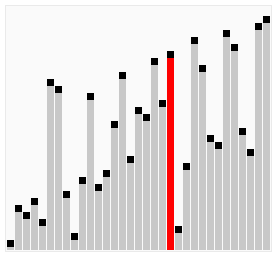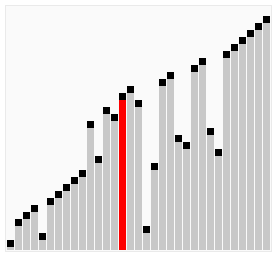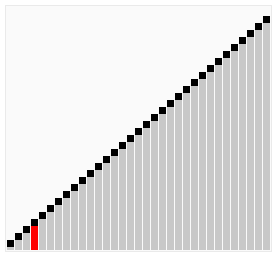
Selction Sort

Definition

• A comparison based sorting algorithm.
  • Starts with the cursor on the left, iterating left to right
  • Compares the left side to the right, looking for the smallest known item
    • If the left is smaller than the item to the right it continues iterating
    • If the left is bigger than the item to the right, the item on the right becomes the known smallest number
    • Once it has checked all items, it moves the known smallest to the cursor and advances the cursor to the right and starts over
  • As the algorithm processes the data set, it builds a fully sorted left side of the data until the entire data set is sorted
• Changes the array in place.

What you need to know

• Inefficient for large data sets.
• Very simple to implement.

Time Complexity

• Best Case Sort: O(n^2)
• Average Case Sort: O(n^2)
• Worst Case Sort: O(n^2)

Space Complexity

• Worst Case: O(1)

Visualization

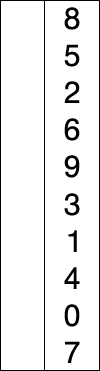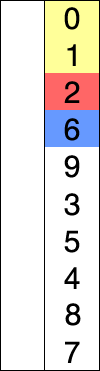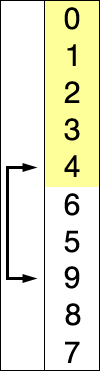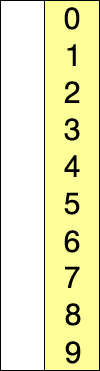
(source: Wikipedia, Selection Sort)

The implementation is here.

Insertion Sort

Definition

• A comparison based sorting algorithm.
  • Iterates left to right comparing the current cursor to the previous item.
  • If the cursor is smaller than the item on the left it swaps positions and the cursor compares itself again to the left hand side until it is put in its sorted position.
  • As the algorithm processes the data set, the left side becomes increasingly sorted until it is fully sorted.
• Changes the array in place.

What you need to know

• Inefficient for large data sets, but can be faster for than other algorithms for small ones.
• Although it has an O(n^2) time complexity, in practice it is slightly less since its comparison scheme only requires checking place if it is smaller than its neighbor.

Time Complexity

• Best Case: O(n)
• Average Case: O(n^2)
• Worst Case: O(n^2)

Space Complexity

• Worst Case: O(n)

Visualization

(source: Wikipedia, Insertion Sort)

The implementation is here.

Merge Sort

Definition

• A divide and conquer algorithm.
  • Recursively divides entire array by half into subsets until the subset is one, the base case.
  • Once the base case is reached results are returned and sorted ascending left to right.
  • Recursive calls are returned and the sorts double in size until the entire array is sorted.

What you need to know

• This is one of the fundamental sorting algorithms.
• Know that it divides all the data into as small possible sets then compares them.

Time Complexity

• Worst Case: O(n log n)
• Average Case: O(n log n)
• Best Case: O(n)

Space Complexity

• Worst Case: O(1)

Visualization

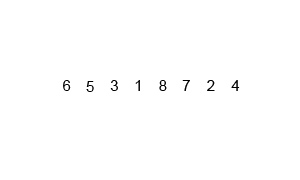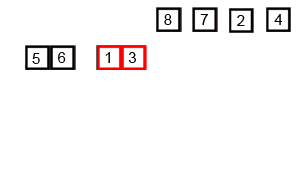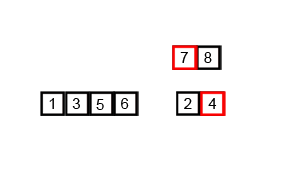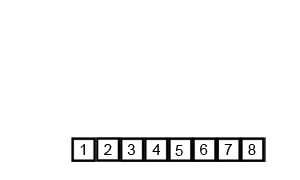
The implementation is here.

Quick sort

Definition

• A divide and conquer algorithm
  • Partitions entire data set in half by selecting a random pivot element and putting all smaller elements to the left of the element and larger ones to the right.
  • It repeats this process on the left side until it is comparing only two elements at which point the left side is sorted.
  • When the left side is finished sorting it performs the same operation on the right side.
• Computer architecture favors the quicksort process.
• Changes the array in place.

What you need to know

• While it has the same Big O as (or worse in some cases) many other sorting algorithms it is often faster in practice than many other sorting algorithms, such as merge sort.

Time Complexity

• Worst Case: O(n^2)
• Average Case: O(n log n)
• Best Case: O(n log n)

Space Complexity

• Worst Case: O(log n)

Visualization

(source: Wikipedia, Quicksort)

Merge Sort Vs. Quicksort

• Quicksort is likely faster in practice, but merge sort is faster on paper.
• Merge Sort divides the set into the smallest possible groups immediately then reconstructs the incrementally as it sorts the groupings.
• Quicksort continually partitions the data set by a pivot, until the set is recursively sorted.

Resources

• https://www.khanacademy.org/computing/computer-science/algorithms
• https://github.com/tsiege/Tech-Interview-Cheat-Sheet#definition-3
• https://minjung-mj-kim.github.io/